들어가며
실수의 표현 방식을 이해하면
실수를 보다 효율적으로
그리고 적절히 사용할 수 있다.
더불어 앞서 제시한 실수의
덧셈에서
오차가 발생한 이유도 알 수 있다.
실수의 표현 방식 - 비하인드
다음 질문에는 어렵지 않게
대답할 수 있다.
"1과 5사이에 존재하는 정수의 개수는?"
그러나 다음 질문에는 답하기가
쉽지 않다.
"1과 2사이에 존재하는 실수의 개수는?"
1과 2 사이에는 무한개의 실수가
존재한다.
따라서 소수점 이하 자릿수까지
표현해야 하는 실수를
컴퓨터로 표현하는 데는 한계가
존재한다.
근데 이게 생각보다 존재감이
엄청나다.
실수의 표현 방식 - 타협과 절충
정수는 오차 없이 표현이 가능하다.
오차 없이 완벽히 양의 정수와
음의 정수를 표현할 수 있다.
그러나 오차를 허용하지 않으면서
그 광대한 실수는 표현하는 것은
불가능하다.
때문에 다음과 같은 결론에
도달하게 된다.
"정밀도를 낮추고, 표현할 수 있는 값의 범위를 넓히자."
그렇다면 정밀도만 낮추면,
즉, 값을 정확히 표현할 수
있는 정도만 낮춘다면,
실수를 폭넓게 표현할 수 있는가?
다음 식을 활용하면 충분히
가능해진다.

위의 식은 컴퓨터의 실수 표현을
위해 약속해 놓은
『IEEE 754』 표준의 이해를 돕기
위한 것이다.
그리고 자바도 이 표준을 따른다.
위 식의 e와 m에 적당한 값을
넣어보자.
예를 들어서, 부호 비트에는
양수를 의미하는 0을,
e에는 00000을, 그리고 m에는
0000000001을 넣어보자.
이때 위 식을 통해서 표현되는
값은 다음과 같다.
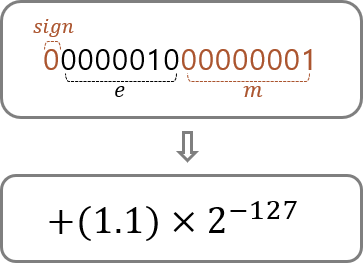
위의 그림을 보면서 이 값이
어느 정도 되는지 감이 오는가?
대충 써보자면 다음과 같다.

표현할 수 있는 값의 범위가
매우 넓어졌음을 알 수 있다.
하지만 분명한 단점도 존재한다.
이러한 표현 방식으로는 위의
숫자 6.46521893 보다
아주 조금 작거나 큰 수를
표현하지 못한다.
이는 m이 1 증가할 때, 전체
값이 얼마나 크게 변경되는지,
그리고 e가 1 증가할 때, 전체
값이 얼마나 크게 변경되는지를
확인하면 쉽게 이해할 수 있다.
즉, 표현할 수 있는 값의 범위는
넓어졌지만
상대적으로 표현하는 대부분의
값에는
오차가 존재하게 되었다.
따라서 다음과 같은 문장을
구성하면,
double num1 = 1.0000001;
double num2 = 2.0000001;[그림 14]의 식을 이용하여,
명시된 수에 최대한 가까운
수가 만들어지도록
비트의 열이 구성되어,
num1과 num2에 저장된다.
때문에 실수에는 항상 오차가
존재한다고 보아야 한다.
참고 및 출처
 |
|


