들어가며
페이스북 같은 소셜 네트워크를
만드다고 하자.
이 애플리케이션에서는 많은
사람이 서로 "친구"가 될 수 있다.
앨리스가 밥의 친구라면 밥 역시
앨리스의 친구이듯
이러한 관계는 상호적이다.
이러한 데이터를 가장 잘 조작하는
방법은 무엇인가?
한 가지 매우 간단한 접근 방식은
2차원 배열로
관계 리스트를 저장하는 것이다.
relationships = [
["Alice", "Bob"],
["Bob", "Cynthia"],
["Alice", "Diana"],
["Bob", "Diana"],
["Elise", "Fred"],
["Diana", "Fred"],
["Fred", "Alice"]
]
불행히도 이 방식으로는 앨리스의
친구가 누구인지 빠르게 알 수가 없다.
배열 내 각 관계를 확인해서 앨리스가
그 관계에 들어있는지 확인해야 한다.
전체 배열을 다 순회해야 앨리스의
전체 친구 리스트가 만들어진다.
그뿐만 아니라 앨리제가 앨리스의
친구인지 간단히 확인하고 싶어도
같은 절차를 밟아야 한다.
위와 같은 방법으로 데이터를
조직하면
앨리스의 친구를 검색할 때
데이터베이스에 있는 모든 관계를
검사해야 하므로
효율성이 O(N)이다.
하지만 훨씬 더 잘 할 수 있다.
그래프라 알려진 자료 구조를
사용하면
앨리스의 모든 친구를 O(1) 시간
만에 찾을 수 있다.
13.1. 그래프
그래프는 데이터가 어떻게 연결되는지
쉽게 이해시키므로
관계에 특화된 자료 구조다.
앞서 다룬 페이스북 네트워크를
그림으로 표현하면 다음과 같다.

한 사람은 노드로, 사람 간 관계는
각 선으로 표현한다.
그래프 용어로 각 노드를 정점이라
부르고, 각 선은 간선이라 부른다.
간선으로 연결된 정점들을 서로
인접하다고 말한다.
그래프를 구현하는 방법은 많지만
가장 간단한 방법 중 하나는 해시
테이블*을 사용하는 것이다.
* 7장 해시 테이블로 매우 빠른 룩업 참고
예제 소셜 네이트워를 대충 루비로
구현해 보면 다음과 같다.
friends = {
"Alice" => ["Bob", "Diana", "Fred"],
"Bob" => ["Alice", "Cynthia", "Diana"],
"Cynthia" => ["Bob"],
"Diana" => ["Alice", "Bob", "Fred"],
"Elise" => ["Fred"],
"Fred" => ["Alice", "Diana", "Elise"]
}
해시 테이블의 모든 키 값은
한 단계로 찾을 수 있으므로
그래프를 쓰면 앨리스의 친구를
O(1)에 찾을 수 있다.
friends["Alice"]
페이스북과 달리 인스타그램에서는
관계가 상호적이지 않다.
즉 앨리스는 밥을 팔로우할 수 있지만,
밥이 만드시 앨리스를 팔로우 하진 않는다.
누가 누구를 팔로우 하는지 보여주는
새로운 그래프를 만들어 보자.

위 예제에서 화살표는 관계의
방향을 나타낸다.
앨리스는 밥과 신시아를 둘 다
팔로우하지만
누구도 앨리스를 팔로우하지
않는다.
밥과 신시아는 서로 팔로우한다.
해시 테이블 방식을 사용하면
코드는 다음과 같을 것이다.
followees = {
"Alice" => ["Bob", "Cynthia"],
"Bob" => ["Cynthia"],
"Cynthia" => ["Bob"]
}
페이스북과 인스타그램 예제는
서로 비슷하지만
각각 관계의 본질이 다르다.
인스타그램의 관계는 방향성이
있으므로
그림으로 표현할 때 화살표를
사용하고,
이러한 그래프를 방향 그래프라
부른다.
페이스북에서는 관계가 상호적이고
단순 선을 사용하므로
그래프를 무방향 그래프라고 부른다.
간단한 해시 테이블로 그래프를
표현할 수 있지만,
보다 강력한 객체 지향 구현도
가능하다.
루비로 보다 강력한 그래프를
구현하면 다음과 같다.
class Person
attr_accessor :name, :friends, :visited
def initialize(name)
@name = name
@friends = []
end
def add_friend(friend)
@friends << friend
end
end
위 루비 클래스로 사람을 만들고
관계를 설정할 수 있다.
mary = Person.new("Mary")
peter = Person.new("Peter")
mary.add_friend(peter)
peter.add_friend(mary)
13.2. 너비 우선 탐색
링크드인은 비즈니스 관계에 특화된
또 다른 인기있는 소셜 네트워크다.
직접 네트워크 외에 2차, 3차
커넥션을 정할 수 있는 부분이
잘 알려진 기능 중 하나다.
다음 그림에서 앨리스는 밥과
직접적인 커넥션이 있고,
밥은 신시아와 직접 커넥션이
있다.
하지만 앨리스는 신시아와 직접
커넥션이 없다.
신시아는 밥을 통해 앨리스와
연결되므로
신시아를 앨리스의 2차 커넥션이라
부른다.

비직접적인 커넥션을 모두 포함해
앨리스의 전체 네트워크를 찾으려면
어떻게 시작해야 할까?
그래프를 순회하는 전형적인 방법은
2가지다.
너비 우선 탐색과 깊이 우선 탐색이다.
이 책은 너비 우선 탐색만 살펴볼
것이며,
깊이 우선 탐색은 스스로 찾아보자.
두 방법은 상당히 유사하고 대부분
똑같이 잘 동작한다.
너비 우선 탐색 알고리즘은
다음으로 처리할 정점을 추적하기
위해 큐*를 사용한다.
* 스택과 큐로 간결한 코드 생성 참고
최초의 큐는 시작점*만 포함한다.
* 여기서는 앨리스
따라서 알고리즘을 시작할 때
큐는 다음과 같을 것이다.
[Alice]
이어서 큐로부터 앨리스를 삭제해서
앨리스 정점을 처리한다.
앨리스 정점에는 "방문함"이라
표시하고,
이 정점을 현재의 정점으로 지정한다*.
* 곧 나올 예제를 따라가다 보면 명확히 이해될 것이다.
이어서 다음의 3단계를 따른다.
- 현재 정점과 인접한 각 정점을 방문한다. 이전에 방문한 적 없는 정점이면 방문했다고 표시하고 큐에 추가한다(이 정점은 아직 현재 정점이 아니다).
- 현재 정점에 인접한 정점을 모두 방문했으면 큐로부터 다음 정점을 제거해서 현재 정점으로 만든다.
- 현재 정점에 인접한 정점을 모두 방문했고 큐에 더 이상 정점이 없으면 알고리즘을 종료한다.
실제로 어떻게 동작하는지 보자.
이어지는 그림 중 첫 번째 그림이
앨리스의 링크드인 네트워크다.

먼저 앨리스를 현재 정점으로
만들면서 시작한다.
두 번째 그림에서 볼 수 있듯이
앨리스를 주황색으로 표시하여
앨리스가 현재 정점임을 표시했다.
또한, 방문했다는 의미로 앨리스에게
체크 부호를 표시했다.

이어서 방문하지 않은 인접 정점인
밥을 방문함으로써
알고리즘을 계속 수행한다.
두 번째 그림처럼 밥의 이름에도
체크 부호를 추가한다.

또한 밥도 큐에 추가한다.
따라서 이제 큐는 [Bob]이다.
다시 말해 아직 밥은 현재 정점이
아니라는 의미다.
중요한 것은 앨리스가 현재 정점
이더라도 여전히 밥을 방문할 수 있다.
다음으로 현재 정점인 앨리스의
인접 정점 중
방문하지 않은 정점이 있는지
확인한다.
캔디가 있으므로 캔디에 방문했다고
표시한다.

이제 큐에는 [Bob, Candy]가
들어 있다.
아직 데릭이라는 방문하지 않은
인접 정점이 앨리스에게 있으므로
데릭에게 방문한다.

이제 큐는 [Bob, Candy, Derek]이다.
하나 남은 방문하지 않은 인접
정점인 일레인을 방문한다.

이제 큐는 [Bob, Candy, Derek, Elaine]이다.
현재 정점인 앨리스의 인접 정점을
모두 방문했으므로
큐에서 정점을 삭제해서 그 정점을
현재 정점으로 만드는
다음 알고리즘 규칙으로 넘어간다.
8장 스택과 큐로 간결한 코드 생성에서
배웠듯이
큐는 앞에서만 데이터를 제거할 수
있고 여기서는 밥이 해당된다.
이제 큐는 [Candy, Derek, Elaine]이고
현재 정점은 밥이다.

현재 정점의 방문하지 않은 인접
정점을 찾는,
첫 번째 규칙으로 돌아간다.
프레드 하나가 있으므로 프레드에
방문했다고 표시하고 큐에 추가한다.

이제 큐는 [Candy, Derek, Elaine, Fred]다.
밥에 더 이상 방문하지 않은 인접
정점이 없으므로
큐에서 다음 정점인 캔디를 삭제해
현재 정점으로 만든다.
큐는 [Derek, Elaine, Fred]이 된다.

하지만 캔디에는 방문하지 않은
인접 정점이 없다.
따라서 큐에서 다음 항목인 데릭을
가져온다.
이제 큐는 [Elaine, Fred]이 된다.

데릭에는 방문하지 않은 인접
정점인 지나가 있으므로
지나에 방문했다고 표시한다.

이제 큐는 [Elaine, Fred, Gina]다.
데릭에는 더 이상 방문하지 않은
인접 정점이 없으므로
큐에서 일레인을 가져와 현재
정점으로 만든다.
이제 큐는 [Fred, Gina]가 된다.

일레인에는 방문하지 않은 인접
정점이 없으므로
큐에서 프레드를 가져온다.
이제 큐는 [Gina]가 된다.

프레드에는 방문할 한 사람,
헬렌이 있으므로
헬렌에 방문했다고 표시하고
큐에 추가하면
큐는 [Gina, Helen]이 된다.

프레드에는 방문하지 않은
커넥션이 더 이상 없으므로
큐에서 지나를 가져와 현재
정점으로 만든다.
이제 큐는 [Helen]이 된다.
지나는 이레나라는 방문할 정점이
하나 있다.

현재 큐는 [Helen, Irena]를 포함한다.
지나는 방문할 커넥션이 없으므로
큐에서 헬렌을 가져와 현재 정점으로
만든다.
이제 큐는 [Irena]가 된다.

헬렌에는 방문할 사람이 없으므로
큐에서 이레나를 가져와 현재
정점으로 만든다.
이제 큐는 []으로 비워진다.

이레나도 방문할 정점이 없고
큐 또한 비었으므로 끝이다.
앞서 구현했던 Person 클래스에
너비 우선 탐색을 사용해
한 사람의 전체 네트워크에 있는
이름을 표시하는
display_network 메서드를
추가하자.
class Person
attr_accessor :name, :friends, :visited
def initialize(name)
@name = name
@friends = []
end
def add_friend(friend)
@friends << friend
end
def display_network
# 방문한 노드를 모두 기록함으로써 알고리즘이 종료됐을 때
# 이러한 노드들의 'visited' 속성을 다시 false로 할당할 수 있다.
to_reset = [self]
# 큐를 생성한다. 처음에는 루트 정점을 포함한다.
queue = [self]
self.visited = true
while queue.any?
# 큐로부터 제거한 정점이 현재 정점이다.
current_vertex = queue.shift
puts current_vertex.name
# 현재 정점의 인접 정점을 모두 큐에 추가한다.
current_vertex.friends.each do |friend|
if !friend.visited
to_reset << friend
queue << friend
friend.visited = true
end
end
end
# 알고리즘이 종료된 후 각 노드의 'visited' 속성을 false로 할당한다.
to_reset.each do |node|
node.visited = false
end
end
end
올바른 동작을 위해 탐색에서
어떤 사람을 방문했는지 기록하는
visited 속성도
Person 클래스에 추가했다.
예제 그래프의 너비 우선 탐색은
다음과 같이 알고리즘의 단계를
2종류로 나눠서
효율성을 계산할 수 있다.
- 큐에서 정점을 삭제해 현재 정점으로 지정한다.
- 각 현재 정점마다 그 정점의 인접 정점을 각각 방문한다.
각 정점은 결국 한 번씩 큐에서
삭제된다.
빅 오 표기법에서는 이를 O(V)라
부른다.
즉, 그래프에 V개의 정점이 있을 때
큐에서 V번 삭제한다.
왜 단순히 정점 개수가 N개 일 때
O(N)이라고 하지 않을까?
위 알고리즘*은 단순히 정점만
처리하는 것이 아니라,
* 그리고 많은 그래프 알고리즘은
간선도 처리하는 단계를 추가로
포함하기 때문이다.
지금부터 설명하겠다.
현재 정점의 각 인접 정점을
몇 번 방문하는지 알아보자.
밥이 현재 정점인 단계만
살펴보자.
이 단계는 다음의 코드를
실행한다.
current_vertex.friends.each do |friend|
if !friend.visited
to_reset << friend
queue << friend
friend.visited = true
end
end
즉, 밥에 인접한 정점을 모두
방문한다.
이때 프레드뿐 아니라 앨리스도
방문한다.
앨리스 정점은 이미 방문했으므로
큐에 넣지는 않지만
each 루프 단계에 포함되기는
마찬가지다.
너비 우선 탐색의 단계를 다시
주의 깊게 살펴보면,
인접한 정점에 방문하는 횟수가
그래프에 있는 간선 수의 2배임을
알 수 있다.
이는 각 간선이 두 정점을 연결하기
때문이며
모든 정점에 대해 인접한 정점을
모두 확인하기 때문이다.
따라서 각 간선은 두 번 쓰인다.
따라서 간선이 E개일 때, 2E번
인접한 정점을 확인한다.
즉 그래프에 간선이 E개 있을 때,
인접한 정점 수의 2배 횟수만큼
확인한다.
하지만 빅 오는 상수를 무시하므로
단순히 O(E)라고 쓴다.
큐에서 제거하는 데 O(V),
방문하는데 O(E)이므로
너비 우선 탐색의 효율성은
O(V+E)이다.
13.3. 그래프 데이터베이스
그래프는 능수능란하게 관계를
처리하므로
데이터를 그래프 형태로 저장하는
DB가 실제로 있다.
전통적인 관계형 데이터 베이스*도
그러한 데이터를 저장할 수 있지만,
소셜 네트워크 같은 데이터를
처리할 때
전통적인 DB와 그래프 DB가
어떻게 성능이 다른지 비교해 보자.
서로가 모두 연결된 다섯 명의
친구로 이뤄진
소셜 네트워크가 있다고 가정하자.
엘리스와 밥, 신디, 데니스, 에델이란
친구들이다.
이들의 정보를 저장할 그래프 DB는
아마 다음과 같을 것이다.

관계형 베이터 베이스를 사용해
위 정보를 저장할 수도 있다.
아마도 두 테이블을 사용할 텐데,
하나는 각 사용자의 개인 정보를,
다른 하나는 친구들 간 관계를
저장할 것이다.
다음은 사용자 테이블이다.

누가 누구와 친구인지 기록하기 위해
별도의 관계 테이블을 사용하겠다.

* 실제로는 이렇게 개별적으로 생성되지 않고 선형적으로 쭉 이어져 있다. 그림이 너무 커지는 관계로 각각의 섹션으로 나누었다.
데이터베이스 이론을 너무 깊게
살펴보지는 않겠지만
이러한 관계 테이블이 각 사용자의
ID를 사용해
어떻게 서로를 표현하는지 알아두자.
이 소셜 네트워크에서는 각각의
사용자가
모든 친구의 개인 정보를 볼 수
있다고 가정하자.
신디가 이러한 정보를 요청한다는
것은
앨리스와, 밥, 데니스, 에델에 대한
모든 정보,
즉 이메일 주소와 전화번호를
알고 싶다는 뜻이다.
관계형 데이터베이스를 기반으로
하는 애플리케이션에서
신디의 요청을 어떻게 실행하는지
보자.
먼저 사용자 테이블에서 신디의
ID를 찾는다.

다음으로 관계 테이블에서 user_id가
3인 모든 줄을 찾는다.

이제 신디의 전체 친구 ID 리스트인
[1, 2, 4, 5]가 생성되었다.
이 ID 리스트로 다시 사용자
테이블에서
ID에 대응하는 각 줄을 찾아야 한다.
컴퓨터가 사용자 테이블에서
각 줄을 찾는 속도는
대략 O(log N)이다.
데이터베이스가 ID 순으로 줄을
관리하고 있으며
데이터베이스가 이진 검색을 사용해
각 줄을 찾을 수 있기 때문이다*.
* 이러한 설명은 특정 관계형 데이터베이스에 해당한다. 관계형 데이터베이스마다 과정이 다를 수 있다.
신디는 친구가 4명이므로 모든
친구의 개인 데이터를 가져오려면
컴퓨터는 O(log N)을 4번 수행해야
한다.
보다 일반적으로 표현하면 친구가
M명일 때,
정보를 가져오는 효율성은
O(M log N)이다.
즉, 각 친구를 검색하는데
log N단계가 걸린다.
위 분석을 그래프 데이터베이스에
기반한 애플리케이션에서
신디의 친구 정보를 알아보는 것과
대조해 보자.
그래프 데이터베이스에서는
데이터베이스에서 신디를 찾기만
하면
한 친구의 정보를 찾는데 딱
한 단계가 걸린다.
데이터베이스 내 각 정점이
그 사용자의 모든 정보를 포함하기
때문이며,
따라서 신디로부터
그녀의 각 친구로 이어지는 간선을
순회하기만 하면 된다.
다음 그림에서 보듯이, 총 4단계가
걸린다.

그래프 데이터베이스에서는 친구가
N명일 때,
데이터를 가져오는 데 O(N)단계가
걸린다.
관계형 데이터 베이스가 제공하는
O(M log N) 효율성에 비해
훨씬 크게 향상되었다.
Neo4j*는 잘 알려진 오픈 소스
그래프 데이터베이스 예제다.
Neo4j 웹사이트에 가서 그래스
데이터베이스에 대한 자료를
더 찾아보길 권한다.
다른 오픈소스 그래프 데이터베이스
예제로는 아랑고 DB*와 아파치 지라프*
등이 있다.
* http://neo4j.com
** http://www.arangoodb.com
*** http://giraph.apache.org
그래프 데이터베이스가 항상
주어진 애플리케이션을 위한
최적의 해결법은 아니다.
각 애플리케이션과 그 요구사항을
주의 깊게 분석해야 한다.
13.4. 가중 그래프
또 다른 종류의 그래프로
가중 그래프가 있다.
가중 그래프는 일반적인 그래프와
비슷하지만
그래프 간의 간선에 추가적인
정보를 제공한다.
다음은 미국의 몇몇 주요 도시에
대한
기본적인 지도를 나타내는 가중
그래프이다.

위 그래프의 각 간선에는
간선이 연결하는 도시 간의
거리를
마일 단위로 표현한 숫자가
붙어 있다.
예를 들어 시카고와 뉴욕 간
거리는 714마일이다.
방향이 있는 가중 그래프도
가능하다.

위 예제의 댈러스에서 토론토로
가는 항공료는 138달러지만
토론토에서 댈러스로 가는 항공료는
216달러 임을 알 수 있다.
그래프에 가중치를 추가하려면
루비 구현을 상당히 수정해야 한다.
특히 배열 대신 해시 테이블을
사용해 인접 노드를 표현할 것이다.
각 정점은 다음 City 클래스로
표현해야 한다.
class City
attr_accessor :name, :routes
def initialize(name)
@name = name
# 배열 대신 해시 테이블로 인접 정점을 표현한다.
@routes = {}
end
def add_route(city, price_info)
@routes[city] = price_info
end
end
이제 도시와 가격이 붙은 경로를
생성할 수 있다.
dallas = City.new("Dallas")
toronto = City.new("Toronto")
dallas.add_route(toronto, 138)
toronto.add_route(dallas, 216)
가중 그래프의 기능을 사용해
최단 경로 문제라 알려진 문제를
해결해 보자.
다음 그래프는 5개 도시 간 가능한
항공료를 보여준다.
항공료가 실제로 저럴리는 없다.

현재는 애틀랜타에 있고, 엘패소로
가고 싶다고 가정하자.
불행히도 직항은 없다.
하지만 다른 도시를 경유해도
괜찮다면 갈 수 있다.
예를 들어 애틀랜타에서 덴버로
가서 덴버에서 엘패소로 갈 수 있다.
이 경로에는 300달러가 든다.
하지만 더 유심히 보면 더 저렴한
경로가 있음을 알 수 있다.
애틀랜타에서 덴버와 시카고를
거쳐 엘패소로 가는 것이다.
비행을 더 해야 하지만 280달러면
된다.
이러한 상황에서 최단 경로 문제란
이런 것이다.
어떻게 하면 가장 적은 돈으로
애틀랜타에서 엘패소로 갈 수 있는가?
13.5. 데이크스트라의 알고리즘
최단 경로 문제를 푸는 알고리즘이
많은데,
1959년, 굉장히 흥미로운 알고리즘
하나를 에드거 데이크스트라가 발견했다.
따라서 이 알고리즘을 데이크스트라의
알고리즘이라 부른다.
다음은 데이크스트라의 알고리즘
규칙이다.
물론 예제로도 살펴볼 때 더욱
명확하게 이해되니 다룰 것이다.
- 시작 정점을 현재 정점으로 한다.
- 현재 정점에 인접한 모든 정점을 확인해서 시작 정점으로부터 알려진 모든 위치까지의 가중치를 계산하고 기록한다.
- 다음 현재 정점을 결정하려면 시작 정점으로부터 도달할 수 있는 방문하지 않은 가장 저렴한 알려진 정점을 찾는다.
- 그래프 내 모든 정점을 방문할 때까지 1~3단계를 반복한다.
위 알고리즘을 단계별로 살펴보자.
애틀랜타부터 다른 도시들까지의
가장 저렴한 경로를 기록하기 위해
다음과 같은 표를 사용하겠다.

먼저 시작 정점인 애틀렌타를
현재 정점으로 한다.
이때 위 알고리즘은 현재 정점과
현재 정점의 인접 정점으로의
연결에만 접근할 수 있다.
정점을 주황색으로 강조하여 한때
현재 정점이었음을 표시하겠다.

다음으로 인접한 정점을 모두
확인해서
시작 점점(애틀랜타)으로부터
알려진 모든 위치까지의 가중치를
기록한다.
애틀랜타부터 보스턴은 100달러에,
애틀랜타로부터 덴버는 160달러에
갈 수 있으므로 이 내용을 표에
기록한다.

다음으로 애틀랜타로부터 갈 수
있는 아직 방문하지 않은
가장 저렴한 정점을 찾는다.
현재로서는 애틀랜타로부터
보스턴과 덴버에 가는 경로만
알고 있으며,
덴버로 가는 것보다 보스턴에
가는 것이 더 저렴하다.
따라서 보스턴을 현재 정점으로
한다.

이어서 보스턴에서 출발하는
두 경로를 확인한 후
시작 정점인 애틀랜타로부터
알려진 모든 위치로 가는
모든 경로의 비용을 새롭게
계산해서 모두 기록한다.
우선 보스턴에서 시카고는
120달러임을 알 수 있다.
또한, 애틀랜타로부터 보스턴은
100달러고
보스턴에서 시카고는 120달러
이므로
애틀랜타로부터 시카고로 가는
가장 저렴한, 그리고 유일한
알려진 경로는 220달러라고
결론 내릴 수 있다.
이를 표에 기록한다.

보스턴에서 다른 경로,
즉 덴버로 가는 경로도 보이는데,
여기는 18-달러다.
이제 애틀랜타에서 덴버로 가는
새로운 경로가 생겼다.
애틀랜타에서 보스턴을 거쳐
덴버로 가는 것이다.
하지만 이 경로는 비용이
280달러지만
애틀랜타에서 덴버로 직항은
160달러다.
표에는 알려진 경로 중 가장
저렴한 경로만 기록하므로
표를 업데이트하지 않는다.
현재 정점인 보스턴에서 갈 수
있는 모든 경로를 알아봤으므로
이제 시작 정점이었던 애틀랜타로
부터 갈 수 있는
가장 저렴한, 방문하지 않은 정점을
찾아본다.
표에 따르면 보스턴은 현재까지
알려진
애틀랜타에서 갈 수 있는 가장
저렴한 도시지만 이미 표시했다.
애틀랜타로부터 220달러가 드는
시카고와 달리
덴버는 160달러만 들기 때문에
덴버가 방문하지 않은
가장 저렴한 도시다.
따라서 덴버가 현재 정점이 된다.
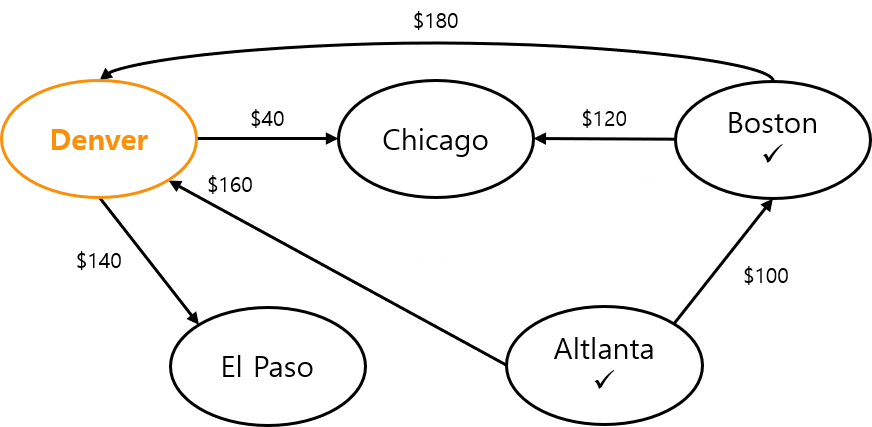
이제 덴버를 떠나는 경로를
검사한다.
한 경로는 덴버에서 시카고로
가는 40달러짜리 비행이다.
애틀랜타에서 시카고로 가는
더 저렴한 경로를 찾았으므로
표를 업데이트할 수 있다.
현재 표에는 애틀랜타에서
시카고로 가는
가장 저렴한 경로가 220달라러고
나와 있지만,
덴버를 거쳐 애틀랜타에서
시카고를 가면 200달러만 든다.
따라서 표를 업데이트한다.

덴버에서 갈 수 있는 다른 경로도
있는데,
새롭게 등장한 도시인 엘패소다.
이제 애틀랜타에서 덴버를 거쳐
엘패소로 가는 300달러 경로다.
이정보도 표에 추가한다.

이제 방문하지 않은 정점이
2개 남았다.
시카고와 엘패소다.
애틀랜타에서 시카고로 가는
알려진, 가장 저렴한 경로*는
애틀랜타에서 엘패소로 가는
알려진, 가장 저렴한 경로**보다 싸다.
* 200달러
** 300달러
따라서 시카고가 다음 현재
정점이 된다.

시카고에서 떠나는 비행기는
딱 하나로
엘패소로 가는 80달러 경로이다.
애틀랜타에서 덴버와 시카고를
거쳐 엘패소로 가는 경로는
총 280달러가 소요되므로 이제
애틀랜타에서 엘패소로 가는
더 저렴한 경로가 생겼다.
새로 발견한 데이터를 표에
업데이트한다.

현재 정점으로 만들 수 있는
알려진 도시가 하나 남았다.
바로 엘패소다.
엘패소에서 떠나는 경로는 딱
하나로,
보스턴으로 가는 100달러짜리
비행이다.
이 데이터가 있어도 애틀랜타에서
다른 도시로 가는
더 저렴한 경로는 찾을 수 없으므로
표를 수정할 필요가 없다.

데이크스트라의 알고리즘을
루비로 구현하면 다음과 같다.
먼저 도시를 표현하는 루비 클래스를
생성한다.
각 도시는 그래프에서 한 노드다.
노드는 그 도시의 이름과 도시로의
경로를 기록한다.
class City
attr_accessor :name, :routes
def initialize(name)
@name = name
# 배열 대신 해시 테이블로 인접 정점을 표현한다.
@routes = {}
# 예제로서 노드가 애틀랜타라면 경로는 다음과 같을 것이다.
# {boston => 100, denver => 160}
end
def add_route(city, price_info)
@routes[city] = price_info
end
end
add_route 메서드를 사용해
예제에 나오는 도시를 설정하겠다.
atlanta = City.new("Atlanta")
boston = City.new("Boston")
chicago = City.new("Chicago")
denver = City.new("Denver")
el_paso = City.new("El Paso")
atlanta.add_route(boston, 100)
atlanta.add_route(denver, 160)
boston.add_route(chicago, 120)
boston.add_route(denver, 180)
chicago.add_route(el_paso, 80)
denver.add_route(chicago, 40)
denver.add_route(el_paso, 140)
데이크스트라의 알고리즘
코드는 다소 복잡하므로
주석을 풍부하게 넣었다.
def dijkstra(starting_city, other_cities)
# route_from_city 해시 테이블은
# 주어진 도시로부터 다른 모든 도시까지의 모든 price_infos 데이터와
# 도착지까지 가는 데 거치는 도시를 포함한다.
routes_from_city = {}
# 위 데이터 포맷은 다음과 같다.
# {도시 => [가격, 원래 도시로부터의 경로 중 이 도시 바로 전에 들르는 도시]}
# 예제에서는 데이터는 다음과 같다.
# {atlanta => [0, nil], boston => [100, atlanta], chicago => [200, denver],
# denver => [160, atlanta], el_paso => [280, chicago]}
# 다음처럼 시작 도시에서 시작 도시로 가는 비용은 0이다.
routes_from_city[starting_city] = [0, starting_city]
# 시작 도시 외에 다른 도시까지 가는 비용과 경로는 아직 알려지지 않았으므로
# 데이터를 초기화할 때 그 밖의 도시에는 모두 무한대 값을 할당한다.
other_cities.each do |city|
routes_from_city[city] = [Float::INFINITY, nil]
end
# 예제의 초기 데이터는 다음과 같다.
# {atlanta => [0, nil], boston => [Float::INFINITY, nil],
# chicago => [Float::INFINITY, nil],
# denver => [Float::INFINITY, nil], el_paso => [Float::INFINITY, nil]}
# 다음 배열에 방문했던 도시를 기록한다.
visited_cities = []
# 시작 도시를 현재 도시로 하여 방문을 시작한다.
current_city = starting_city
# 알고리즘의 핵심부. 즉, 각 도시를 방문하는 루프를 시작한다.
while current_city
# 정식으로 현재 도시를 방문한다.
# 방문한 도시 헤시 테이블에 현재 도시를 추가한다.
visited_cities << current_city
# 현재 도시로부터 각 경로를 확인한다.
current_city.routes.each do |city, price_info|
# 시작 도시에서 다른 도시로 경로가 routes_from_city에 현재 기록된 값보다
# 저렴하면 업데이트 한다.
if routes_from_city[city][0] > price_info + routes_from_city[current_city][0]
routes_from_city[city] = [price_info + routes_from_city[current_city][0], current_city]
end
end
# 다음으로 방문할 도시를 정한다.
current_city = nil
cheapest_route_from_current_city = Float::INFINITY
# 가능한 모든 경로를 확인한다.
routes_from_city.each do |city, price_info|
# 이 경로가 현재 도시로부터의 가장 저렴한 경로이고, 아직 방문하지 않았다면,
# 다음으로 방문할 도시가 된다.
if price_info[0] < cheapest_route_from_current_city && !visited_cities.include?(city)
cheapest_route_from_current_city = price_info[0]
current_city = city
end
end
end
return routes_from_city
end
다음과 같이 위 메서드를
실행시킨다.
routes = dijkstra(atlanta, [boston, chicago, denver, el_paso])
routes.each do |city, price_info|
p "#{city.name}: #{price_info[0]}"
end
이 예제는 가장 저렴한 비행
경로를 찾는데 초점을 맞췄지만
매핑과 GPS 기술에도 동일한
방식을 사용할 수 있다.
각 간선의 가중치를 가격이 아닌
각 도시에서 다른 도시로 운전할 때
얼마나 빨리 갈 수 있으냐로
표현한다면
쉽게 데이크스트라의 알고리즘을
사용해
한 장소에서 다른 장소로 운전할
때 어떤 경로로 가야할 지
결정할 수 있다.
13.6. 마무리
이 책에서 다룰 마지막 주요
자료구조를 13장에서 다뤘으니
우리의 여정도 거의 끝나간다.
그래프는 관계를 포함하는 데이터를
처리할 때 매우 강력한 도구이며,
코드 속도를 높임과 동시에 까다로운
문제를 푸는데 도움이 될 수 있음을
알아보았다.
지금까지 줄곧 주된 관심사는 코드를
얼마나 빨리 실행시키는가였다.
즉, 시간 관점에서 코드가 얼마나
효율적으로 실행되는지 측정했고,
알고리즘에 걸리는 단계 수가
측정 기준이었다.
하지만 다른 방식으로도 효율성을
측정할 수 있다.
어떤 경우에는 속도보다 더 큰
관심사가 있을 수 있으며,
자료 구조나 알고리즘이 얼마나
많은 메모리를 소비하느냐가
중요할 수도 있다.
14장에서는 공간 관점에서 코드의
효율성을 분석하는 법을 배우겠다.
참고 및 출처
 |
|



