비선형 자료구조
비선형 자료구조란 일렬로 나열하지 않고
자료 순서나 관계가 복잡한 구조를 말한다.
일반적으로 트리나 그래프를 말한다.
그래프(Graph)
그래프는 정점과 간선으로 이루어진
자료구조를 말한다.
정점과 간선
어떠한 곳에서 어떠한 곳으로 무언가를 통해
간다고 했을 때,
'어떠한 곳'은 정점(Vertex)이 되고 '무언가'는
간선(Edge)가 된다.

이때 두 정점 간에 한 쪽으로만 방향성을
가진 간선을 '단방향 간선'이라고 하며,
두 정점 간에 양 쪽으로 방향성을 가진
간선을 '양방향 간선'이라고 한다.
그래프는 이러한 성질들을 가지고
다음과 같은 모습을 나타낸다.

정점으로 나가는 간선을 해당 정점의
outdegree라고 하며,
들어오는 간선을 해당 정점의
indegree라고 한다.
위 그림의 정점 V는 outdegree 3개,
indegree 2개인 상태이다.
또한 정점은 약자로 V 또는 U라고 하며,
보통 어떤 정점으로부터 시작해서 어떤
정점가지 간다를
"U에서부터 V로 간다." 라고 표현한다.
지금까지 설명한 정점과 간선으로 이루어진
집합을 그래프라고 한다.
가중치(Weight)
가중치는 간선과 정점 사이에드는 비용을
뜻한다.
1번 노드와 2번 노드까지 가는 비용이
한 칸이라면
1번 노드에서 2번 노드까지의 가중치는
한 칸이다.
예를 들어, U에서 V로 가는 데 걸리는 택시비가 13,000원이라면 가중치는 13,000원이다.
트리(Tree)
트리는 그래프의 특수한 형태 중 하나로,
그래프의 특징처럼 정점과 간선을 가지고
트리 구조로 배열된
일종의 계층적 데이터의 집합이다.
트리의 특징

트리는 그래프의 일종이며, 다음 특징을
가진다는 점이 다르다.
- 부모, 자식 계층 구조를 가진다.
- 'V - 1 = E'라는 특징이 있다. 간선 수는 '노드 수 - 1'이다.
- 임의의 두 노드 사이의 경로는 반드시 단 하나만 존재한다. 즉, 트리 내의 어떤 노드와 어떤 노드까지의 경로는 반드시 존재한다.
트리의 구성
트리는 루트노드 내부노드 리프노드로
이루어져 있다.
- 루트 노드: 최상위에 있는 노드를 의미한다.
- 내부 노드: 루트 노드와 리프 노드 사이, 또는 루트 노드와 내부 노드 사이에 있는 노드를 의미한다.
- 리프 노드: 자식 노드가 없는 노드를 의미한다.
트리의 높이와 레벨

- 깊이: 트리에서의 깊이는 각 노드마다 다르며, 루트 노드부터 특정 노드까지 최단 거리로 갔을 때의 거리를 말한다.
- 높이: 트리의 높이는 루트 노드로부터 리프 노드까지 거리 중 가장 긴 거리를 의미한다.
- 레벨: 트리의 레벨은 주어지는 문제마다 조금씩 다르지만 보토 깊이와 같은 의미를 지닌다.
- 서브 트리: 트리 내의 하위 집합을 서브 트리라고 한다. 트리 내에 있는 부분집합이라고도 보면 된다.
이진 트리
이진 트리는 자식의 노드 수가 두 개 이하인
트리를 의미하며, 이를 다음과 같이 분류한다.
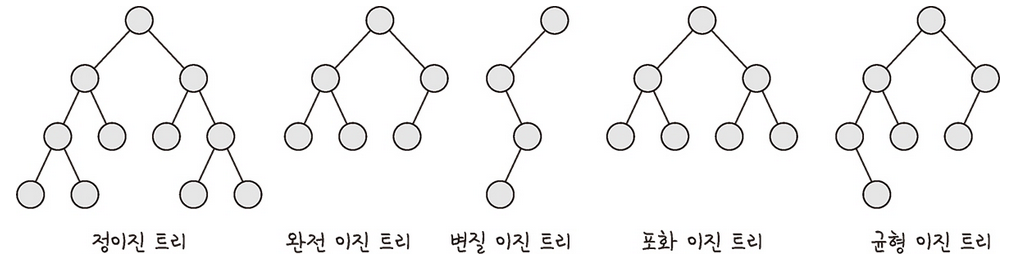
- 정 이진 트리(Full Binary Tree): 자식 노드가 0 또는 2개인 이진 트리를 의미한다.
- 완전 이진 트리(Complete Binary Tree): 왼쪽에서부터 채워져 있는 이진 트리를 의미한다. 마지막 레벨을 제외하고는 모든 레벨이 완전히 채워져 있으며, 마지막 레벨의 경우 왼쪽부터 채워져 있다.
- 변질 이진 트리(Degenerate Binary Tree): 자식 노드가 하나밖에 없는 이진 트리를 의미한다.
- 포화 이진 트리(Perfect Binary Tree): 모든 노드가 꽉 차있는 이진 트리를 의미힌다.
- 균형 이진 트리(Balanced Binary Tree): 왼쪽과 오른쪽 노드의 높이 차이가 1 이하인 이진 트리를 의미힌다. map, set을 구성하는 레드 블랙 트리는 균형 이진 트리 중 하나다.
이진 탐색 트리(Binary Search Tree)
이진 탐색 트리(BST)는 노드의 오른쪽
하위 트리에는 '노드 값보다 큰 값'이,
왼쪽 하위 트리에는 '노드 값보다 작은 값'이
들어 있는 트리를 말한다.
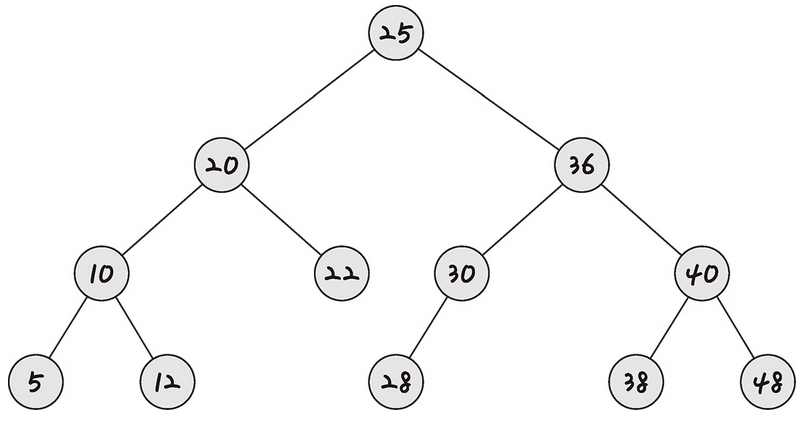
이때 왼쪽 및 오른쪽 하위 트리도
해당 특성을 갖는다.
이렇게 두면 '검색'을 하기에 용이하다.
왼쪽에는 작은 값, 오른쪽에는 큰 값이
이미 정해져 있기 때문에
10을 찾으려고 한다면 25의 왼쪽 노드들만
찾으면 된다는 것은 자명하다.
보통 요소를 찾을 때 이진 탐색 트리의 경우
O(log n)이 걸린다.
하지만 최악의 경우 O(n)이 걸린다.
그 이유는 이진 탐색 트리는 삽입 순서에 따라
선형적일 수 있기 때문이다.
예를 들어 다음 그림과 같다.

AVL 트리(Adelson-Velsky and Landis Tree)
AVL 트리는 앞서 설명한 최악의 경우
선형적인 트리가 되는 것을 방지하고
스스로 균형을 잡는 이진 탐색 트리이다.
두 자식 서브 트리 높이는 항상 최대 1만큼
차이가 난다는 특징이 있다.

이진 탐색 트리는 선형적인 트리 형태를
가질 때
최악의 경우 O(n)의 시간 복잡도를 가진다.
"이러한 최악의 경우를 배제하고 항상 균형잡힌 트리로 만들자."
라는 개념을 가진 트리가 바로 AVL 트리다.
탐색, 삽입, 삭제 모두 시간 복잡도가
O(log n)이며,
삽입, 삭제를 할 때마다 균형이 안 맞는 것을
맞추기 위해
트리 일부를 횐쪽 혹은 오른쪽으로 회전시키며
균형을 잡는다.
레드-블랙 트리(Red-Black Tree)
레드-블랙 트리는 균형 이진 탐색 트리로
탐색, 삽압, 삭제 모두
시간 복잡도가 O(log n)이다.

각 노드는 빨간색 또는 검은 색의 색상을 나타내는
추가 비트를 저장하며,
삽입 및 삭제 중에 트리가 균형을 유지하도록
하는데 사용된다.
C++ STL의 set, multiset, map, multimap이
레드-블랙 트리를 이용하여 구현되었다.
힙(Heap)
힙은 완전 이진 트리 기반의 자료구조이며,
최소힙과 최대힙 두 가지가 있고
해당 힙에 따라 특정한 특징을 지킨
트리를 말한다.
- 최대힙: 루트 노드에 있는 키는 모든 자식에 있는 키 중에서 가장 커야 한다. 또한, 각 노드의 자식 노드와의 관계에도 이와 같으 특징이 재귀적으로 이루어져야 한다.
- 최소힙: 최소 힙에서 루트 노드에 있는 키는 모든 자식에 있는 키 중에서 최솟값이어야 한다. 또한, 각 노드의 자식 노드와의 관계도 이와 같은 특징이 재귀적으로 이루어져야 한다.
힙에는 어떠한 값이 들어와도 특정 힙의
규칙을 지키게 만들어져 있다.
예를 들어 최대 힙을 기반으로 설명하면
다음과 같다.
최대힙의 삽입
힙에 새로운 요소가 들어오면,
일단 새로운 노드를 힙의 마지막 노드에
이어서 삽입한다.
이 새로운 노드를 부모 노드들과의 크기를
비교하며 교환해서 힙의 성질을 만족시킨다.

예를 들어 8이라는 값으 가진 노드 밑에 15라는
값을 가진 노드를 삽입하면
이 노드가 점차 올라가면서 해당 노드와 스왑하는
과정을 거쳐 최대힙 조건을 만족한다.
최대힙의 삭제
최대힙에서 최댓값은 루트노드이므로
루트 노드가 삭제되고,
그 이후 마지막 노드와 루트 노드를 스왑하여
또 다시 스왑 등의 과정을 거쳐 재구성된다.
우선순위 큐(Priority Queue)
우선순위 큐는 우선 순위 대기열이라고도 하며,
대기열에서 우선순위가 높은 요소가 우선순위가
낮은 요소보다 먼저 제공되는 자료구조이다.

우선순위 큐는 힙을 기반으로 구현된다.
맵(Map)
맵은 특정 순서에 따라 키와 매핑된
값의 조합으로 형성된 자료구조이다.
셋(Set)
셋은 특정 순서에 따라 고유한 요소를
저장하는 컨테이너이며,
중복되는 요소는 없고 오로지 희소한
값만 저장하는 자료구조이다.
해시 테이블(Hash Table)
해시 테이블은 무한에 가까운 데이터들을
유한한 개수의 해시 값으로 매핑한 테이블이다.
삽입, 삭제, 탐색 시 평균적으로 O(1)의
시간 복잡도를 가진다.
<면접을 위한 CS 전공지식 노트>



